Solutions to jamb mathematics number bases questions

Spread the love

For the best guide in your studies and mathematics tutorials with videos, visit ogschools.com

1979-7: In base ten, the number 101101(base 2) equals

Solution

${ 101101 }_{ 2 }\\ 1\times { 2 }^{ 5 }+0\times { 2 }^{ 4 }+1\times 2^{ 3 }+1\times { 2 }^{ 2 }+0\times { 2 }^{ 1 }+1\times { 2 }^{ 0 }\\ 32+8+4+1\\ { 45 }_{ 10 }$

1980-49: Write the decimal number 39 t0 base 2

Solution

2	39	R
2	19	1
2	9	1
2	4	1
2	2	0
2	1	0
	0	1

$\therefore \quad Ans={ 100111 }_{ 2 }$

1983-21: Find x if ${ ({ x }_{ 4 }) }^{ 2 }={ 100100 }_{ 2 }$

Solution

${ x }_{ 4 }=x\times { 4 }^{ 0 }=x\\ { 100100 }_{ 2 }=1\times { 2 }^{ 5 }+1\times { 2 }^{ 2 }=32+4=36\\ { x }^{ 2 }=36\\ x=6$

4	6	R
4	1	2
	0	1

$Ans={ 12 }_{ 4 }$

1984-12: A trader in a country where their currency ‘MONI'(M) is in base five bought ${ 103 }_{ 5 }$ oranges at ${ M14 }_{ 5 }$ each. If he sold the oranges at ${ M24 }_{ 5 }$ each, what will be his gain?

Solution

$total\quad price\quad of\quad oranges\quad bought:\quad 103\times 24=3032\\ total\quad price\quad of\quad oranges\quad sold:\quad 103\times 14=2002\\ gain:\quad 3032-2002=1030\\ \therefore \quad Ans={ M1030 }_{ 5 }\\$

1985-3: In the equation below, solve for x if all the numbers are in base 2: $\frac { 11 }{ x } =\frac { 1000 }{ x+101 }$ , leaving your answer in base 2.

Solution

$\frac { 11 }{ x } =\frac { 1000 }{ x+101 } \\ { 11 }_{ 2 }=1\times { 2 }^{ 1 }+1\times { 2 }^{ 0 }=2+1=3\\ { 1000 }_{ 2 }=1\times { 2 }^{ 3 }=8\\ { 101 }_{ 2 }=1\times { 2 }^{ 2 }+1\times { 2 }^{ 0 }=5\\ \frac { 3 }{ x } =\frac { 8 }{ x+5 } \\ 3x+15=8x\\ 15=8x-3x\\ 5x=15\\ x={ 3 }_{ 10 }$

2	3	R
2	1	1
	0	1

$\therefore \quad Ans={ 11 }_{ 2 }$

1986-1: Evaluate ${ 212 }_{ 3 }-{ 121 }_{ 3 }+{ 222 }_{ 3 }\\$

Solution

${ 212 }_{ 3 }-{ 121 }_{ 3 }={ 101 }_{ 3 }\\ { 212 }_{ 3 }+101={ 1020 }_{ 3 }\\ \therefore \quad Ans={ 1020 }_{ 3 }\\$

1987-1: Convert 241 in base 5 to base 8

Solution

${ 241 }_{ 5 }=2\times { 5 }^{ 2 }+4\times { 5 }^{ 1 }+1\times { 5 }^{ 0 }=50+20+1=71\\$

8	71	R
8	8	7
8	1	0
	0	1

$\therefore \quad Ans={ 107 }_{ 8 }$

1991-2: If 2257 is the result of subtracting 4577 from 7056 in base n, find n

Solution

${ 7056 }_{ n }-{ 4577 }_{ n }={ 2257 }_{ n }\\ 7\times { n }^{ 3 }+5\times { n }_{ 1 }+6\times { n }^{ 0 }-(4\times { n }^{ 3 }+5\times { n }^{ 2 }+7\times { n }^{ 1 }+7\times { n }^{ 0 })=2\times { n }^{ 3 }+2\times { n }^{ 2 }+5\times { n }^{ 1 }+7\times { n }^{ 0 }\\ 7{ n }^{ 3 }+5n+6-{ 4n }^{ 3 }-5{ n }^{ 2 }-7n-7=2{ n }^{ 3 }+2{ n }^{ 2 }+5n+7\\ 3{ n }^{ 3 }-5{ n }^{ 2 }-2n-1=2{ n }^{ 3 }+2{ n }^{ 2 }+5n+7\\ { n }^{ 3 }-7{ n }^{ 2 }-7n=8\\ \therefore n=8\\$

1992-1: Find n if { 34 }_{ n }= ${ 10011 }_{ 2 }\\$

Solution

${ 34 }_{ n }={ 10011 }_{ 2 }\\ 3\times { n }^{ 1 }+4\times { n }^{ 0 }=1\times { 2 }^{ 4 }+1\times { 2 }^{ 1 }+1\times { 2 }^{ 0 }\\ 3n+4=19\\ 3n=19-4\\ 3n=15\\ n=5$

1993-1: Change ${ 71 }_{ 10 }$ to base 8

Solution

8	71	R
8	8	7
8	1	0
	0	1

$\therefore Ans={ 107 }_{ 8 }$

1995-1: Calculate ${ 3310 }_{ 5 }-{ 1442 }_{ 5 }$

Solution

${ 3310 }_{ 5 }-{ 1442 }_{ 5 }={ 1313 }_{ 5 }$

1997-1: If ${ (1p03) }_{ 4 }={ 115 }_{ 10 }$ , find p

Solution

${ 1p03 }_{ 4 }={ 115 }_{ 10 }\\ 1\times { 4 }^{ 3 }+p\times { 4 }^{ 2 }+3\times { 4 }^{ 0 }=115\\ 64+16p+3=115\\ 16p=115-67\\ 16p=48\\ p=3$

1998-1: If ${ 1011 }_{ 2 }+{ x }^{ 7 }={ 25 }_{ 10 }$ , solve for x

Solution

${ 1011 }_{ 2 }+{ x }^{ 7 }={ 25 }_{ 10 }\\ 1\times { 2 }^{ 3 }+1\times { 2 }^{ 1 }+1\times { 2 }^{ 0 }+x\times { 2 }^{ 0 }=25\\ 8+2+1+x=25\\ 11+x=25\\ x=14$

1999-1: ${ 2 }_{ 9 }\times { (y3) }_{ 9 }={ 3 }_{ 5 }\times { (y3) }_{ 5 }$ . Find the value of y

Solution

${ 2 }_{ 9 }\times { (y3) }_{ 9 }={ 3 }_{ 5 }\times { (y3) }_{ 5 }\\ 2\times (9y+3)=3\times (5y+3)\\ 18y+6=15y+9\\ 3y=3\\ y=1$

1999-2: Divide ${ 2434 }_{ 6 }\quad by\quad { 42 }_{ 6 }$ and leave your answer in base 6

Solution

${ 2434 }_{ 6 }=2\times { 6 }^{ 3 }+4\times { 6 }^{ 2 }+3\times { 6 }^{ 1 }+4\\ =432+144+18+4\\ =598\\ { 42 }_{ 6 }=4\times { 6 }^{ 1 }+2=26\\ \frac { 598 }{ 26 } ={ 23 }_{ 10 }$

6	23	R
6	3	5
	0	3

$\therefore \quad Ans={ 35 }_{ 6 }$

2000-8: If ${ p344 }_{ 6 }-{ 23p2 }_{ 6 }={ 2pp2 }_{ 6 }$ , find the value of digit p

Solution

${ p344 }_{ 6 }=p\times { 6 }^{ 3 }+3\times { 6 }^{ 2 }+4\times { 6 }^{ 1 }+4\times { 6 }^{ 0 }\\ =216p+108+24+4\\ =216p+136\\ { 23p2 }_{ 6 }=2\times { 6 }^{ 3 }+3\times { 6 }^{ 2 }+p\times 6+2\\ =432+108+6p+2\\ =6p+542\\ { 2pp2 }_{ 6 }=2\times { 6 }^{ 3 }+p\times { 6 }^{ 2 }+p\times { 6 }^{ 1 }+2\times { 6 }^{ 0 }\\ =432+36p+6p+2\\ =42p+434\\ \therefore 216p+136-(6p+542)=42p+434\\ 210p-406=42p+434\\ 168p=840\\ p=5$

2000-11: If ${ 314 }_{ 10 }-{ 256 }_{ 7 }={ 340 }_{ x }$ , find x

Solution

${ 314 }_{ 10 }=314\\ { 256 }_{ 7 }=2\times { 7 }^{ 2 }+5\times { 7 }^{ 1 }+6\times { 7 }^{ 0 }=98+35+6=139\\ { 340 }_{ x }=3\times { x }^{ 2 }+4\times { x }^{ 1 }=3{ x }^{ 2 }+4x\\ \therefore \quad 314-139=3{ x }^{ 2 }+4x\\ 3{ x }^{ 2 }+4x-175=0\\ a=3,\quad b=4,\quad c=-175\\ x=\frac { -b\pm \sqrt { { b }^{ 2 }-4ac } }{ 2a } \\ substituting\quad the\quad values\quad of\quad a,b\quad and\quad c\\ x=7\quad or\quad \frac { -50 }{ 6 } \\ since\quad x\quad can't\quad be\quad a\quad negative\quad number\quad or\quad fraction,\\ then\quad x=7\\$

2003-5: Simplify ${ 213 }_{ 4 }\times { 23 }_{ 4 }$

Solution

$\therefore \quad Ans=12231$

2003-7: The sum of four numbers is ${ 1214 }_{ 5 }$ . What is the average expressed in base five?

Solution

${ 1214 }_{ 5 }=1\times { 5 }^{ 3 }+2\times { 5 }^{ 2 }+1\times { 5 }^{ 1 }+4\times { 5 }^{ 0 }\\ =125+50+5+4\\ =184\\ \frac { 184 }{ 4 } ={ 46 }_{ 10 }\\$

5	46	R
5	9	1
5	1	4
	0	1

$\therefore \quad Ans={ 141 }_{ 5 }$

2004-2: Find p, if ${ 451 }_{ 6 }-{ p }_{ 7 }={ 305 }_{ 6 }$

Solution

${ 451 }_{ 6 }-{ p }_{ 7 }={ 305 }_{ 6 }\\ { p }_{ 7 }={ p }_{ 6 }\\ { 451 }_{ 6 }-{ p }_{ 6 }={ 305 }_{ 6 }\\ { p }_{ 6 }={ 451 }_{ 6 }-{ 305 }_{ 6 }\\ { p }_{ 6 }={ 142 }_{ 6 }\\ { 142 }_{ 6 }=1\times { 6 }^{ 2 }+4\times { 6 }^{ 1 }+2=36+24+2={ 62 }_{ 10 }\\$

7	62	R
7	8	6
7	1	1
	0	1

$\therefore \quad Ans={ 116 }_{ 7 }$

2005-1: Find the value of m if ${ 13 }_{ m }+{ 24 }_{ m }={ 41 }_{ m }$

Solution

${ 13 }_{ m }+{ 24 }_{ m }={ 41 }_{ m }\\ m+3+2m+4=4m+1\\ 3m+7=4m+1\\ m=6$

2005-2: If ${ 321 }_{ 4 }$ is divided by ${23}_{4}$ and leaves a remainder r, what is the value of r?

Solution

${ 321 }_{ 4 }=3\times { 4 }^{ 2 }+2\times { 4 }^{ 1 }+1\times { 4 }^{ 0 }=48+8+1=57\\ { 23 }_{ 4 }=2\times { 4 }^{ 1 }+3\times { 4 }^{ 0 }=8+3=11\\ \frac { 57 }{ 11 } =5\quad remainder\quad 2\\ { 2 }_{ 10 }={ 2 }_{ 4 }\\ \therefore \quad r=2$

2006-34: If ${ (k2) }_{ 6 }\times { 3 }_{ 6 }={ 3 }_{ 5 }\times { (k4) }_{ 5 }$ , what is the value of k?

Solution

${ (k2) }_{ 6 }\times { 3 }_{ 6 }={ 3 }_{ 5 }\times { (k4) }_{ 5 }\\ (6k+2)3=3(5k+4)\\ 18k+6=15k+12\\ 3k=6\\ k=2$

2006-36: Convert ${ 2232 }_{ 4 }$ to a number in base 6

Solution

${ 2232 }_{ 4 }=2\times { 4 }^{ 3 }+2\times { 4 }^{ 2 }+3\times { 4 }^{ 1 }+2\\ =128+32+12+2\\ ={ 174 }_{ 10 }$

6	174	R
6	29	0
6	4	5
	0	4

$\therefore \quad Ans={ 450 }_{ 6 }$

2006-39: compute ${ 110011 }_{ 2 }+{ 11111 }_{ 2 }$

Solution

2007-49: If ${ x }_{ 10 }={ 1214 }_{ 5 }$ , find x

Solution

${ x }_{ 10 }={ 1214 }_{ 5 }\\ x=1\times { 5 }^{ 3 }+2\times { 5 }^{ 2 }+1\times { 5 }^{ 1 }+4\times { 5 }^{ 0 }\\ x=125+50+5+4\\ x=184$

2008-2: If ${ 125 }_{ x }={ 20 }_{ 10 }$ , find x

Solution

${ 125 }_{ x }={ 20 }_{ 10 }\\ { x }^{ 2 }+2x+5=20\\ { x }^{ 2 }+2x-15=0\\ { x }^{ 2 }+5x-3x-15=0\\ ({ x }^{ 2 }+5x)-(3x+15)=0\\ x(x+5)-3(x+5)=0\\ (x-3)(x+5)=0\\ x=3\quad or\quad -5\\ since\quad x\quad can't\quad be\quad negative,\\ x=3$

2009-2: If ${ 55 }_{ x }+{ 52 }_{ x }={ 77 }_{ 10 }$ , find x

Solution

${ 55 }_{ x }+{ 52 }_{ x }={ 77 }_{ 10 }\\ 5x+5+5x+2=77\\ 10x+7=77\\ 10x=70\\ x=7$

2010-2: Find r, if ${ 6r7 }_{ 8 }={ 511 }_{ 9 }$

Solution

{ 6r7 }_{ 8 }={ 511 }_{ 9 }\\ { 6r7 }_{ 8 }=6\times { 8 }^{ 2 }+r\times { 8 }^{ 1 }+7\times { 8 }^{ 0 }=384+8r+7=391+8r\\ { 511 }_{ 9 }=5\times { 9 }^{ 2 }+1\times 9+1=405+9+1=415\\ 391+8r=415\\ 8r=415-391\\ 8r=24\\ r=3

2012-2: If ${ 2q3 }_{ 5 }={ 77 }_{ 8 }$ , find q

Solution

${ 2q3 }_{ 5 }={ 77 }_{ 8 }\\ 2\times 25+5q+3=56+7\\ 50+5q+3=63\\ 5q=10\\ q=2$

This is as much as we can take on this topic. If you feel there’s any other question on this topic giving you problem feel free to drop it. Be rest assured that it will be solved. No one is above errors, notify us if you feel there was an error in any of the calculations

Comments

Nelson says

May 5, 2021 at 4:47 pm

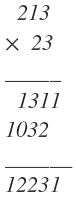
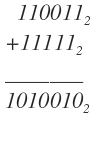
I really enjoy your write-up it’s really helpful. thank you keep up the good work

- Prettylifestylez says
  
  May 10, 2021 at 8:04 pm
  
  Thanks. I’m glad you liked it
  
Promise says

September 21, 2021 at 8:52 pm

It really helpful,I enjoyed it 🤔

Master C Brown says

October 8, 2021 at 4:50 pm

Your solutions are unique

Victoria says

November 21, 2021 at 4:32 am

1992-1

Why is the answer 15? Is 25-11=15
I thought it is 14

- Prettylifestylez says
  
  November 30, 2021 at 12:27 pm
  
  It was an error
  
Abdulfatah Fatima says

March 3, 2022 at 9:23 pm

Help me with this

4243 base 5 – 13×4 base 5 = y 244 base 5. Find x and y

Rosie Smith says

April 6, 2022 at 10:20 pm

I don’t get your 2012, number 2, can you explain in details

Sadeeq says

April 8, 2022 at 9:54 am

Great work.

James Uche says

April 8, 2022 at 2:13 pm

It’s very lovely, and I really appreciate it, the problem I have is how can study well for the subject I don’t know to well,for instance I have problem with Chemistry

Neo says

June 29, 2022 at 7:09 pm

This is very helpful. Thanks a lot dear. God bless you.

1979-7: In base ten, the number 101101(base 2) equals

Solution

1980-49: Write the decimal number 39 t0 base 2

Solution

1983-21: Find x if { ({ x }_{ 4 }) }^{ 2 }={ 100100 }_{ 2 }

Solution

1984-12: A trader in a country where their currency ‘MONI'(M) is in base five bought { 103 }_{ 5 } oranges at { M14 }_{ 5 } each. If he sold the oranges at { M24 }_{ 5 } each, what will be his gain?

Solution

1985-3: In the equation below, solve for x if all the numbers are in base 2: \frac { 11 }{ x } =\frac { 1000 }{ x+101 } , leaving your answer in base 2.

Solution

1986-1: Evaluate { 212 }_{ 3 }-{ 121 }_{ 3 }+{ 222 }_{ 3 }\\

Solution

1987-1: Convert 241 in base 5 to base 8

Solution

1991-2: If 2257 is the result of subtracting 4577 from 7056 in base n, find n

Solution

1992-1: Find n if { 34 }_{ n }={ 10011 }_{ 2 }\\

Solution

1993-1: Change { 71 }_{ 10 } to base 8

Solution

1995-1: Calculate { 3310 }_{ 5 }-{ 1442 }_{ 5 }

Solution

1997-1: If { (1p03) }_{ 4 }={ 115 }_{ 10 }, find p

Solution

1998-1: If { 1011 }_{ 2 }+{ x }^{ 7 }={ 25 }_{ 10 }, solve for x

Solution

1999-1: { 2 }_{ 9 }\times { (y3) }_{ 9 }={ 3 }_{ 5 }\times { (y3) }_{ 5 }. Find the value of y

Solution

1999-2: Divide { 2434 }_{ 6 }\quad by\quad { 42 }_{ 6 } and leave your answer in base 6

Solution

2000-8: If { p344 }_{ 6 }-{ 23p2 }_{ 6 }={ 2pp2 }_{ 6 }, find the value of digit p

Solution

2000-11: If { 314 }_{ 10 }-{ 256 }_{ 7 }={ 340 }_{ x }, find x

Solution

2003-5: Simplify { 213 }_{ 4 }\times { 23 }_{ 4 }

Solution

2003-7: The sum of four numbers is { 1214 }_{ 5 }. What is the average expressed in base five?

Solution

2004-2: Find p, if { 451 }_{ 6 }-{ p }_{ 7 }={ 305 }_{ 6 }

Solution

2005-1: Find the value of m if { 13 }_{ m }+{ 24 }_{ m }={ 41 }_{ m }

Solution

2005-2: If { 321 }_{ 4 } is divided by {23}_{4} and leaves a remainder r, what is the value of r?

Solution

2006-34: If { (k2) }_{ 6 }\times { 3 }_{ 6 }={ 3 }_{ 5 }\times { (k4) }_{ 5 }, what is the value of k?

Solution

2006-36: Convert { 2232 }_{ 4 } to a number in base 6

Solution

2006-39: compute { 110011 }_{ 2 }+{ 11111 }_{ 2 }

Solution

2007-49: If { x }_{ 10 }={ 1214 }_{ 5 }, find x

Solution

2008-2: If { 125 }_{ x }={ 20 }_{ 10 }, find x

Solution

2009-2: If { 55 }_{ x }+{ 52 }_{ x }={ 77 }_{ 10 }, find x

Solution

2010-2: Find r, if { 6r7 }_{ 8 }={ 511 }_{ 9 }

Solution

2012-2: If { 2q3 }_{ 5 }={ 77 }_{ 8 }, find q

Solution

Comments

Trackbacks

Leave a Reply Cancel reply

1983-21: Find x if ${ ({ x }_{ 4 }) }^{ 2 }={ 100100 }_{ 2 }$

1984-12: A trader in a country where their currency ‘MONI'(M) is in base five bought ${ 103 }_{ 5 }$ oranges at ${ M14 }_{ 5 }$ each. If he sold the oranges at ${ M24 }_{ 5 }$ each, what will be his gain?

1985-3: In the equation below, solve for x if all the numbers are in base 2: $\frac { 11 }{ x } =\frac { 1000 }{ x+101 }$ , leaving your answer in base 2.

1986-1: Evaluate ${ 212 }_{ 3 }-{ 121 }_{ 3 }+{ 222 }_{ 3 }\\$

1992-1: Find n if { 34 }_{ n }= ${ 10011 }_{ 2 }\\$

1993-1: Change ${ 71 }_{ 10 }$ to base 8

1995-1: Calculate ${ 3310 }_{ 5 }-{ 1442 }_{ 5 }$

1997-1: If ${ (1p03) }_{ 4 }={ 115 }_{ 10 }$ , find p

1998-1: If ${ 1011 }_{ 2 }+{ x }^{ 7 }={ 25 }_{ 10 }$ , solve for x

1999-1: ${ 2 }_{ 9 }\times { (y3) }_{ 9 }={ 3 }_{ 5 }\times { (y3) }_{ 5 }$ . Find the value of y

1999-2: Divide ${ 2434 }_{ 6 }\quad by\quad { 42 }_{ 6 }$ and leave your answer in base 6

2000-8: If ${ p344 }_{ 6 }-{ 23p2 }_{ 6 }={ 2pp2 }_{ 6 }$ , find the value of digit p

2000-11: If ${ 314 }_{ 10 }-{ 256 }_{ 7 }={ 340 }_{ x }$ , find x

2003-5: Simplify ${ 213 }_{ 4 }\times { 23 }_{ 4 }$

2003-7: The sum of four numbers is ${ 1214 }_{ 5 }$ . What is the average expressed in base five?

2004-2: Find p, if ${ 451 }_{ 6 }-{ p }_{ 7 }={ 305 }_{ 6 }$

2005-1: Find the value of m if ${ 13 }_{ m }+{ 24 }_{ m }={ 41 }_{ m }$

2005-2: If ${ 321 }_{ 4 }$ is divided by ${23}_{4}$ and leaves a remainder r, what is the value of r?

2006-34: If ${ (k2) }_{ 6 }\times { 3 }_{ 6 }={ 3 }_{ 5 }\times { (k4) }_{ 5 }$ , what is the value of k?

2006-36: Convert ${ 2232 }_{ 4 }$ to a number in base 6

2006-39: compute ${ 110011 }_{ 2 }+{ 11111 }_{ 2 }$

2007-49: If ${ x }_{ 10 }={ 1214 }_{ 5 }$ , find x

2008-2: If ${ 125 }_{ x }={ 20 }_{ 10 }$ , find x

2009-2: If ${ 55 }_{ x }+{ 52 }_{ x }={ 77 }_{ 10 }$ , find x

2010-2: Find r, if ${ 6r7 }_{ 8 }={ 511 }_{ 9 }$

2012-2: If ${ 2q3 }_{ 5 }={ 77 }_{ 8 }$ , find q